Table of Contents
dsift.h implements a dense version of SIFT. This is an object that can quickly compute descriptors for densely sampled keypoints with identical size and orientation. It can be reused for multiple images of the same size.
Overview
- See also
- The SIFT module, Technical details
This module implements a fast algorithm for the calculation of a large number of SIFT descriptors of densely sampled features of the same scale and orientation. See the SIFT module for an overview of SIFT.
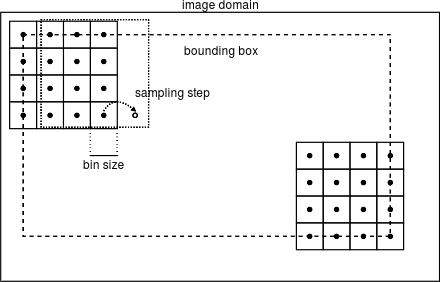
The feature frames (keypoints) are indirectly specified by the sampling steps (vl_dsift_set_steps) and the sampling bounds (vl_dsift_set_bounds). The descriptor geometry (number and size of the spatial bins and number of orientation bins) can be customized (vl_dsift_set_geometry, VlDsiftDescriptorGeometry).
By default, SIFT uses a Gaussian windowing function that discounts contributions of gradients further away from the descriptor centers. This function can be changed to a flat window by invoking vl_dsift_set_flat_window. In this case, gradients are accumulated using only bilinear interpolation, but instad of being reweighted by a Gassuain window, they are all weighted equally. However, after gradients have been accumulated into a spatial bin, the whole bin is reweighted by the average of the Gaussian window over the spatial support of that bin. This “approximation” substantially improves speed with little or no loss of performance in applications.
Keypoints are sampled in such a way that the centers of the spatial bins are at integer coordinates within the image boundaries. For instance, the top-left bin of the top-left descriptor is centered on the pixel (0,0). The bin immediately to the right at (binSizeX,0), where binSizeX is a paramtere in the VlDsiftDescriptorGeometry structure. vl_dsift_set_bounds can be used to further restrict sampling to the keypoints in an image.
Usage
DSIFT is implemented by a VlDsiftFilter object that can be used to process a sequence of images of a given geometry. To use the DSIFT filter:
- Initialize a new DSIFT filter object by vl_dsift_new (or the simplified vl_dsift_new_basic). Customize the descriptor parameters by vl_dsift_set_steps, vl_dsift_set_geometry, etc.
- Process an image by vl_dsift_process.
- Retrieve the number of keypoints (vl_dsift_get_keypoint_num), the keypoints (vl_dsift_get_keypoints), and their descriptors (vl_dsift_get_descriptors).
- Optionally repeat for more images.
- Delete the DSIFT filter by vl_dsift_delete.
Technical details
This section extends the SIFT descriptor section and specialzies it to the case of dense keypoints.
Dense descriptors
When computing descriptors for many keypoints differing only by their position (and with null rotation), further simplifications are possible. In this case, in fact,
\begin{eqnarray*} \mathbf{x} &=& m \sigma \hat{\mathbf{x}} + T,\\ h(t,i,j) &=& m \sigma \int g_{\sigma_\mathrm{win}}(\mathbf{x} - T)\, w_\mathrm{ang}(\angle J(\mathbf{x}) - \theta_t)\, w\left(\frac{x - T_x}{m\sigma} - \hat{x}_i\right)\, w\left(\frac{y - T_y}{m\sigma} - \hat{y}_j\right)\, |J(\mathbf{x})|\, d\mathbf{x}. \end{eqnarray*}
Since many different values of T are sampled, this is conveniently expressed as a separable convolution. First, we translate by \( \mathbf{x}_{ij} = m\sigma(\hat x_i,\ \hat y_i)^\top \) and we use the symmetry of the various binning and windowing functions to write
\begin{eqnarray*} h(t,i,j) &=& m \sigma \int g_{\sigma_\mathrm{win}}(T' - \mathbf{x} - \mathbf{x}_{ij})\, w_\mathrm{ang}(\angle J(\mathbf{x}) - \theta_t)\, w\left(\frac{T'_x - x}{m\sigma}\right)\, w\left(\frac{T'_y - y}{m\sigma}\right)\, |J(\mathbf{x})|\, d\mathbf{x}, \\ T' &=& T + m\sigma \left[\begin{array}{cc} x_i \\ y_j \end{array}\right]. \end{eqnarray*}
Then we define kernels
\begin{eqnarray*} k_i(x) &=& \frac{1}{\sqrt{2\pi} \sigma_{\mathrm{win}}} \exp\left( -\frac{1}{2} \frac{(x-x_i)^2}{\sigma_{\mathrm{win}}^2} \right) w\left(\frac{x}{m\sigma}\right), \\ k_j(y) &=& \frac{1}{\sqrt{2\pi} \sigma_{\mathrm{win}}} \exp\left( -\frac{1}{2} \frac{(y-y_j)^2}{\sigma_{\mathrm{win}}^2} \right) w\left(\frac{y}{m\sigma}\right), \end{eqnarray*}
and obtain
\begin{eqnarray*} h(t,i,j) &=& (k_ik_j * \bar J_t)\left( T + m\sigma \left[\begin{array}{cc} x_i \\ y_j \end{array}\right] \right), \\ \bar J_t(\mathbf{x}) &=& w_\mathrm{ang}(\angle J(\mathbf{x}) - \theta_t)\,|J(\mathbf{x})|. \end{eqnarray*}
Furthermore, if we use a flat rather than Gaussian windowing function, the kernels do not depend on the bin, and we have
\begin{eqnarray*} k(z) &=& \frac{1}{\sigma_{\mathrm{win}}} w\left(\frac{z}{m\sigma}\right), \\ h(t,i,j) &=& (k(x)k(y) * \bar J_t)\left( T + m\sigma \left[\begin{array}{cc} x_i \\ y_j \end{array}\right] \right), \end{eqnarray*}
(here \( \sigma_\mathrm{win} \) is the side of the flat window).
- Note
- In this case the binning functions \( k(z) \) are triangular and the convolution can be computed in time independent on the filter (i.e. descriptor bin) support size by integral signals.
Sampling
To avoid resampling and dealing with special boundary conditions, we impose some mild restrictions on the geometry of the descriptors that can be computed. In particular, we impose that the bin centers \( T + m\sigma (x_i,\ y_j) \) are always at integer coordinates within the image boundaries. This eliminates the need for costly interpolation. This condition amounts to (expressed in terms of the x coordinate, and equally applicable to y)
\[ \{0,\dots, W-1\} \ni T_x + m\sigma x_i = T_x + m\sigma i - \frac{N_x-1}{2} = \bar T_x + m\sigma i, \qquad i = 0,\dots,N_x-1. \]
Notice that for this condition to be satisfied, the descriptor center \( T_x \) needs to be either fractional or integer depending on \( N_x \) being even or odd. To eliminate this complication, it is simpler to use as a reference not the descriptor center T, but the coordinates of the upper-left bin \( \bar T \). Thus we sample the latter on a regular (integer) grid
\[ \left[\begin{array}{cc} 0 \\ 0 \end{array}\right] \leq \bar T = \left[\begin{array}{cc} \bar T_x^{\min} + p \Delta_x \\ \bar T_y^{\min} + q \Delta_y \\ \end{array}\right] \leq \left[\begin{array}{cc} W - 1 - m\sigma N_x \\ H - 1 - m\sigma N_y \end{array}\right], \quad \bar T = \left[\begin{array}{cc} T_x - \frac{N_x - 1}{2} \\ T_y - \frac{N_y - 1}{2} \\ \end{array}\right] \]
and we impose that the bin size \( m \sigma \) is integer as well.